Contenido

• Pasos
• Consejos

La función racional tiene la forma y = N (x) / D (x), donde N y D son polinomios. Para trazar una función de este tipo con precisión, necesita un buen conocimiento de álgebra, incluidos los cálculos diferenciales. Considere el siguiente ejemplo: y = (2X - 6X + 5)/(4X + 2).

Pasos

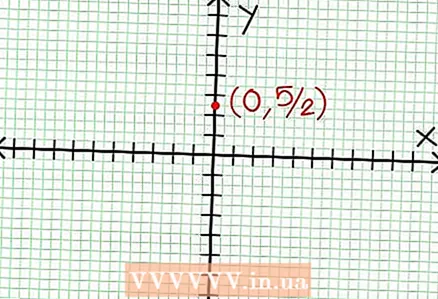1. 1 Encuentra la intersección con el eje y de la gráfica. Para hacer esto, sustituya x = 0 en la función y obtenga y = 5/2. Por tanto, el punto de intersección del gráfico con el eje Y tiene coordenadas (0, 5/2).Coloque este punto en el plano de coordenadas.
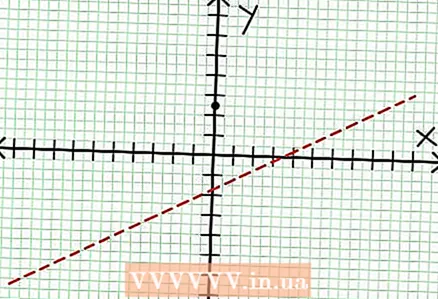2. 2 Encuentra las asíntotas horizontales. Divida el numerador por el denominador (en una columna) para determinar el comportamiento de "y" con valores de "x" que tienden a infinito. En nuestro ejemplo, la división será y = (1/2)X - (7/4) + 17/(8X + 4). Para valores grandes positivos o negativos de "x" 17 / (8X + 4) tiende a cero y la gráfica se aproxima a la línea recta dada por la función y = (1/2)X - (4/7). Utilizando la línea de puntos, trace esta función.
   • Si el grado del numerador es menor que el grado del denominador, entonces no puede dividir el numerador por el denominador y la asíntota será descrita por la función a = 0.
   • Si el grado del numerador es igual al grado del denominador, entonces la asíntota es una línea horizontal igual a la razón de los coeficientes en "x" en el grado más alto.
   • Si el grado del numerador es 1 más que el grado del denominador, entonces la asíntota es una línea recta inclinada, cuya pendiente es igual a la relación de los coeficientes en "x" al grado más alto.
   • Si el grado del numerador es mayor que el grado del denominador en 2, 3, etc., entonces para valores grandes |NS| sentido a tienden al infinito (positivo o negativo) en forma de cuadrado, cúbico u otro grado de polinomio. En este caso, lo más probable es que no necesite construir una gráfica exacta de la función obtenida al dividir el numerador por el denominador.
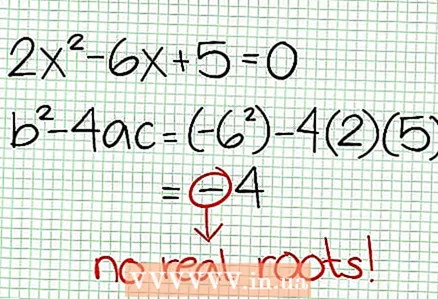3. 3 Encuentra los ceros de la función. Una función racional tiene ceros cuando su numerador es cero, es decir, N (NS) = 0. En nuestro ejemplo, 2X - 6X + 5 = 0. El discriminante de esta ecuación cuadrática: B - 4C.A = 6 - 4 * 2 * 5 = 36 - 40 = -4. Dado que el discriminante es negativo, entonces N (NS), y por tanto F (NS) no tiene raíces reales. La gráfica de una función racional no se cruza con el eje X. Si la función tiene ceros (raíces), colóquelos en el plano de coordenadas.
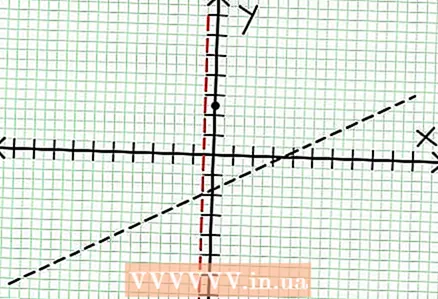4. 4 Encuentra las asíntotas verticales. Para hacer esto, establezca el denominador en cero. En nuestro ejemplo, 4X + 2 = 0 y NS = -1/2. Trace la asíntota vertical usando la línea de puntos. Si por algún valor NS N (NS) = 0 y D (NS) = 0, entonces la asíntota vertical existe o no existe (este es un caso raro, pero es mejor recordarlo).
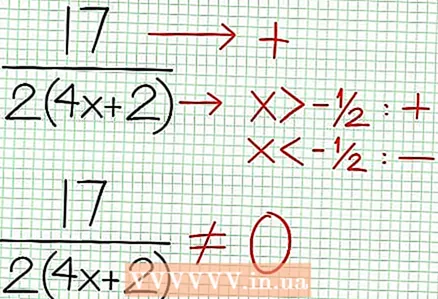5. 5 Mira el resto del numerador dividido por el denominador. ¿Es positivo, negativo o cero? En nuestro ejemplo, el resto es 17, que es positivo. Denominador 4X + 2 positivo a la derecha de la asíntota vertical y negativo a la izquierda de la misma. Esto significa que la gráfica de la función racional para valores positivos grandes NS se aproxima a la asíntota desde arriba, y para valores negativos grandes NS - desde abajo. Desde 17 / (8X + 4) nunca es igual a cero, entonces la gráfica de esta función nunca intersecará la línea recta especificada por la función a = (1/2)NS - (7/4).
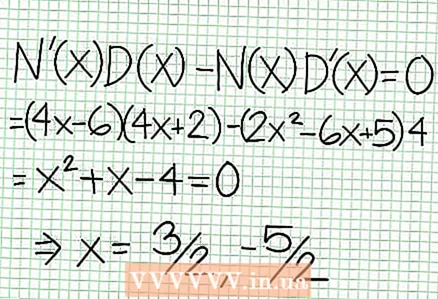6. 6 Encuentra extremos locales. Existe un extremo local para N '(X) D (X) - N (X) D '(X) = 0. En nuestro ejemplo, N ’(X) = 4X - 6 y D '(X) = 4. N ’(X) D (X) - N (X) D '(X) = (4X - 6)(4X + 2) - (2X - 6X + 5)*4 = X + X - 4 = 0. Resolviendo esta ecuación, encuentras que X = 3/2 y X = -5/2. (Estos no son valores del todo precisos, pero son adecuados para nuestro caso cuando no se necesita superprecisión).
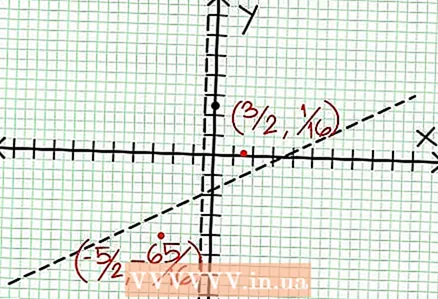7. 7 Encuentra el valor a para cada extremo local. Para hacer esto, sustituya los valores NS en la función racional original. En nuestro ejemplo, f (3/2) = 1/16 y f (-5/2) = -65/16. Aparte los puntos (3/2, 1/16) y (-5/2, -65/16) en el plano de coordenadas. Dado que los cálculos se basan en valores aproximados (del paso anterior), el mínimo y el máximo encontrados tampoco son del todo precisos (pero probablemente muy cerca de los valores exactos). (El punto (3/2, 1/16) está muy cerca del mínimo local. A partir del paso 3, sabemos que a siempre positivo para NS> -1/2, y encontramos un valor pequeño (1/16); por lo tanto, el valor de error es extremadamente pequeño en este caso).
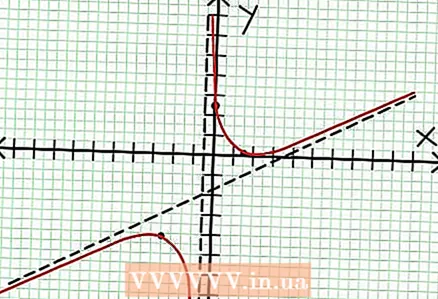8. 8 Conecte los puntos pendientes y extienda suavemente el gráfico a las asíntotas (no se olvide de la dirección correcta del gráfico acercándose a las asíntotas). Recuerde que el gráfico no debe cruzar el eje X (consulte el paso 3). El gráfico tampoco se cruza con las asíntotas horizontal y vertical (consulte el paso 5). No cambie la dirección del gráfico excepto en los puntos extremos encontrados en el paso anterior.

Consejos

• Si siguió los pasos anteriores estrictamente en orden, entonces no es necesario calcular las segundas derivadas (o cantidades complejas similares) para probar su solución.
• Si no necesita calcular los valores de las cantidades, puede reemplazar la búsqueda de extremos locales calculando algunos pares de coordenadas adicionales (NS, a) entre cada par de asíntotas. Además, si no le importa cómo funciona el método descrito, no se sorprenda de por qué no puede encontrar la derivada y resolver la ecuación N '(X) D (X) - N (X) D '(X) = 0.
• En algunos casos, tendrá que trabajar con polinomios de orden superior. Si no puede encontrar la solución exacta usando factorización, fórmulas, etc., calcule las posibles soluciones usando métodos numéricos como el método de Newton.
• En casos raros, el numerador y el denominador comparten un factor variable común. De acuerdo con los pasos descritos, esto conducirá a cero y una asíntota vertical en el mismo lugar. Sin embargo, esto no es posible y la explicación es una de las siguientes:
  • Cero en N (NS) tiene una multiplicidad mayor que cero en D (NS). Gráfico F (NS) tiende a cero en este punto, pero no se define allí. Indíquelo dibujando un círculo alrededor del punto.
  • Cero en N (NS) y cero en D (NS) tienen la misma multiplicidad. El gráfico se acerca a un punto distinto de cero en este valor. NSpero no definido en el mismo. Indíquelo dibujando un círculo alrededor del punto.
  • Cero en N (NS) tiene una multiplicidad menor que cero en D (NS). Aquí hay una asíntota vertical.