Contenido

• Al paso
• Método 1 de 3: una primera tarea sencilla
• Método 2 de 3: cálculo del valor esperado para un resultado específico
• Método 3 de 3: comprender el concepto
• Consejos
• Artículos de primera necesidad

El valor de la expectativa es un término estadístico y un concepto que se utiliza para decidir qué tan útil o dañina será una acción. Para calcular el valor esperado, es necesario obtener una buena comprensión de cada resultado en una situación particular y la probabilidad asociada, o la probabilidad de que ocurra un resultado particular. Los pasos a continuación proporcionan algunos ejercicios de ejemplo para ayudarlo a comprender el concepto de valor esperado.

Al paso

Método 1 de 3: una primera tarea sencilla

1. Lea la declaración. Antes de empezar a pensar en todos los posibles resultados y probabilidades, es importante que comprenda el problema. Por ejemplo, un juego de dados que cuesta 10 € por juego. Se lanza un dado hexagonal una vez y sus ganancias dependen del número que saque. Si sale un 6, gana 30 €; un 5 gana 20 €; cualquier otro número no da nada.
2. Enumere todos los resultados posibles. Ayuda enumerar todos los resultados posibles en una situación determinada. En el ejemplo anterior, hay 6 resultados posibles. Estos son: (1) saca un 1 y pierdes $ 10, (2) saca un 2 y pierdes $ 10, (3) saca un 3 y pierdes $ 10, (4) saca un 4 y pierdes $ 10 , (5) saque un 5 y gane $ 10, (6) saque un 6 y gane $ 20.
   • Tenga en cuenta que cada resultado es 10 € menos que el descrito anteriormente, ya que primero tendrá que pagar 10 € por juego, independientemente del resultado.
3. Determine la probabilidad de cada resultado. En este caso, la probabilidad de 6 resultados es la misma. La probabilidad de que salga un número aleatorio es de 1 en 6. Para facilitar la escritura, escribiremos la fracción (1/6) como decimal usando una calculadora: 0,167. Escriba esta probabilidad junto a cada resultado, especialmente si desea resolver un problema con diferentes probabilidades para cada resultado.
   • Tu calculadora 1/6 podría generar algo como 0.166667. Redondeamos esto a 0,167 para facilitar el cálculo sin sacrificar la precisión.
   • Si desea un resultado muy preciso, no lo convierta en un decimal, simplemente ingrese 1/6 en la fórmula y calcúlelo en su calculadora.
4. Registre el valor de cada resultado. Multiplique el $ de un resultado por la probabilidad de que ocurra el resultado para calcular cuánto dinero contribuirá ese resultado al valor esperado. Por ejemplo, el resultado de sacar un 1 es - $ 10 y la probabilidad de sacar un 1 es 0,167. Por lo tanto, el valor de lanzar un 1 es (-10) * (0.167).
   • No es necesario calcular estos resultados ahora si tiene una calculadora que puede realizar varias operaciones al mismo tiempo. Obtendrá un resultado más preciso si ingresa la ecuación completa.
5. Agregue el valor de cada resultado para obtener el valor esperado de un evento. Para continuar con el ejemplo anterior, el valor esperado del juego de dados es: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), o -1,67 €. Por lo tanto, puede esperar perder $ 1.67 cada vez en este juego (por juego).
6. ¿Cuáles son las implicaciones de calcular el valor esperado? En el ejemplo anterior, determinamos que la ganancia (pérdida) esperada sería de -1,67 € por lanzamiento. Este es un resultado imposible para 1 juego; puede perder 10 €, ganar 10 € o ganar 20 €. Pero a largo plazo, el valor esperado es una probabilidad media útil. Si sigues jugando a este juego, perderás alrededor de $ 1,67 por juego, en promedio. Otra forma de pensar en el valor esperado es asignando ciertos costos (o beneficios) al juego; solo debes jugar a este juego si consideras que vale la pena, disfrútalo lo suficiente como para gastar $ 1.67 en él cada vez.
   • Cuanto más a menudo se repite una situación, con mayor precisión el valor esperado es una representación del resultado promedio real. Por ejemplo, tal vez juegue el juego 5 veces seguidas y pierda cada vez, lo que resulta en una pérdida promedio de $ 10. Sin embargo, si juega el juego 1000 veces más, el resultado promedio se acercará cada vez más al valor esperado de -1,67 € por juego. Este principio se llama "la ley de los grandes números".

Método 2 de 3: cálculo del valor esperado para un resultado específico

1. Utilice este método para calcular la cantidad promedio de monedas que necesita lanzar antes de que ocurra un patrón en particular. Por ejemplo, puede usar el método para averiguar la cantidad esperada de monedas para lanzar hasta que tenga caras dos veces seguidas. Este problema es un poco más complicado que un problema estándar sobre valores esperados, así que lea primero la parte anterior de este artículo si no está familiarizado con el concepto de valor esperado.
2. Supongamos que buscamos un valor x. Está tratando de determinar cuántas monedas tiene que lanzar en promedio para obtener dos caras seguidas. Ahora hacemos una comparación para encontrar la respuesta. Llamamos x a la respuesta que buscamos. Hacemos la comparación necesaria paso a paso. Actualmente tenemos lo siguiente:
   • x = ___
3. Piense en lo que sucede si el primer lanzamiento produce una moneda. Este será el caso en la mitad de los casos. Si este es el caso, ha "desperdiciado" una vuelta, mientras que la posibilidad de dar la vuelta dos veces seguidas no ha cambiado. Al igual que con el lanzamiento de una moneda, se espera que tenga que lanzar un número promedio de veces antes de obtener una cara dos veces seguidas. En otras palabras, esperaría lanzar un número x de veces, más las que ya ha jugado. En forma de ecuación:
   • x = (0,5) (x + 1) + ___
   • Vamos a llenar el espacio vacío mientras seguimos pensando en otras situaciones.
   • Puede usar fracciones en lugar de decimales si es más fácil o necesario.
4. Piense en lo que sucede cuando lanza la cabeza. Existe una probabilidad de 0.5 (o 1/2) de que lances una taza la primera vez. Esto parece acercarse al objetivo de lanzar una cabeza dos veces seguidas, pero ¿cuánto? La forma más fácil de averiguarlo es pensar en sus opciones en el segundo rollo:
   • Si el segundo lanzamiento es una moneda, volvemos al principio.
   • Si la segunda vez también es una taza, ¡hemos terminado!
5. Aprenda a calcular la probabilidad de que ocurran dos eventos. Ahora sabemos que tienes un 50% de posibilidades de que lances una taza, pero ¿cuál es la probabilidad de que lances una taza dos veces seguidas? Para calcular esta probabilidad, multiplique la probabilidad de ambos. En este caso es 0,5 x 0,5 = 0,25. Por supuesto, esta es también la posibilidad de que salga cara y luego cruz, porque ambas tienen una probabilidad de 0,5 de ocurrir: 0,5 x 0,5 = 0,25.
6. Suma el resultado de "cara, luego cruz" a la ecuación. Ahora que hemos calculado la probabilidad de que ocurra este evento, podemos pasar a expandir la ecuación. Existe una probabilidad de 0,25 (o 1/4) de que desperdiciemos lanzando dos veces sin avanzar. Pero ahora todavía necesitamos un número x de lanzamientos más en promedio para obtener el resultado que queremos obtener, más los 2 que ya lanzamos. En forma de ecuación, esto se convierte en (0.25) (x + 2), que ahora podemos agregar a la ecuación:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + ___
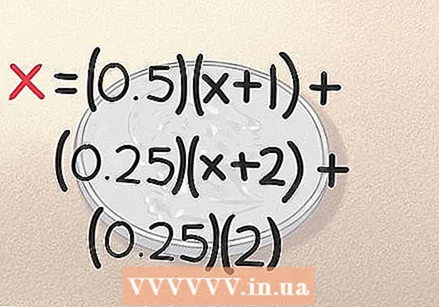7. Agregue el resultado de "encabezado, encabezado" a la ecuación. Si rueda la cabeza, la cabeza con los dos primeros lanzamientos de las monedas, ya está. Obtuviste el resultado en exactamente 2 lanzamientos. Como señalamos anteriormente, existe una probabilidad de 0.25 de que esto suceda, por lo que la ecuación para esto es (0.25) (2). Nuestra comparación ahora está completa:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + (0,25) (2)
   • Si no está seguro de haber pensado en todas las situaciones posibles, existe una manera fácil de verificar que la ecuación esté completa. El primer número en cada parte de la ecuación representa la probabilidad de que ocurra un evento. Esto siempre sumará 1. Aquí, 0.5 + 0.25 + 0.25 = 1, entonces sabemos que hemos incluido todas las situaciones.
8. Simplifica la ecuación. Hagamos la ecuación un poco más fácil multiplicando. Recuerde, si ve algo entre paréntesis como esto: (0.5) (x + 1), entonces multiplique 0.5 por cada término que esté en el segundo conjunto de paréntesis. Esto le da lo siguiente: 0.5x + (0.5) (1) o 0.5x + 0.5. Hagamos esto para cada término de la ecuación, luego combinemos estos términos para que todo parezca un poco más simple:
   • x = 0.5x + (0.5) (1) + 0.25x + (0.25) (2) + (0.25) (2)
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0,75x + 1,5
9. Solución para x. Como en cualquier ecuación, necesitarás aislar la x en un lado de la ecuación para calcularla. Recuerde, x significa "la cantidad promedio de monedas que necesita lanzar para obtener cara dos veces seguidas". Cuando hemos calculado x, también hemos encontrado nuestra respuesta.
   • x = 0,75x + 1,5
   • x - 0,75x = 0,75x + 1,5 - 0,75x
   • 0,25 veces = 1,5
   • (0,25 aumentos) / (0,25) = (1,5) / (0,25)
   • x = 6
   • En promedio, tendrás que lanzar una moneda 6 veces antes de lanzar cara dos veces.

Método 3 de 3: comprender el concepto

1. ¿Qué es un valor esperado en realidad? El valor esperado no es necesariamente el resultado más obvio o lógico. A veces, un valor esperado puede ser incluso un valor imposible en una situación determinada. Por ejemplo, el valor esperado puede ser de + 5 € para un juego con un premio de no más de 10 €. Lo que indica el valor esperado es cuánto valor tiene un evento en particular. Si un juego tiene un valor esperado de + € 5, puede jugarlo si cree que vale la pena el tiempo y el dinero que puede obtener por juego. Si otro juego tiene un valor esperado de - $ 20, solo lo jugará si cree que cada juego vale $ 20.
2. Comprender el concepto de eventos independientes. En la vida cotidiana, muchos de nosotros pensamos que tenemos un día de suerte cuando suceden algunas cosas buenas, y esperamos que el resto del día sea así.De la misma manera, podemos pensar que ya hemos tenido suficiente de un accidente y que realmente hay que hacer algo divertido ahora. Matemáticamente, las cosas no salen así. Si lanza una moneda normal, existe exactamente la misma posibilidad de que arroje una cara o una moneda. No importa cuántas veces hayas lanzado; la próxima vez que lo lances seguirá funcionando de la misma manera. El lanzamiento de la moneda es "independiente" de los otros lanzamientos, no se ve afectado por él.
   • La creencia de que puedes tener suerte o mala suerte al lanzar monedas (o cualquier otro juego de azar), o El hecho de que toda tu mala suerte haya terminado y la suerte esté de tu lado también se llama trampa del jugador (o falacia del jugador). Esto tiene que ver con la tendencia de las personas a tomar decisiones arriesgadas o estúpidas cuando sienten que la suerte está de su lado, o si sienten "racha de suerte" o si sienten que "su suerte está a punto de cambiar" ".
3. Comprende la ley de los grandes números. Podría pensar que el valor esperado no es realmente útil, porque rara vez le dice cuál es el resultado real de una situación. Si ha calculado que el valor esperado de un juego de ruleta es -1 €, y juega el juego 3 veces, normalmente terminará con -10 €, o + 60 €, o algún otro resultado. La "Ley de los números grandes" ayuda a explicar por qué el valor esperado es más útil de lo que piensas: cuanto más juegues, más cerca del valor esperado será el resultado promedio. Cuando observa la gran cantidad de eventos, es muy probable que el resultado final se acerque al valor esperado.

Consejos

• Para aquellas situaciones en las que son posibles múltiples resultados, puede crear una hoja de cálculo en la computadora para calcular el valor esperado usando los resultados y sus probabilidades.
• Los cálculos de € anteriores también funcionan en otras monedas.

Artículos de primera necesidad

• Lápiz
• Papel
• Calculadora