Contenido

• Pasos
• Método 1 de 3: Cómo resolver una ecuación cúbica sin un término constante
• Método 2 de 3: Cómo encontrar raíces enteras usando multiplicadores
• Método 3 de 3: Cómo resolver una ecuación usando el discriminante

En una ecuación cúbica, el exponente más alto es 3, dicha ecuación tiene 3 raíces (soluciones) y tiene la forma ${ Displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Algunas ecuaciones cúbicas no son tan fáciles de resolver, pero si aplica el método correcto (con una buena base teórica), puede encontrar las raíces de incluso la ecuación cúbica más compleja; para esto, use la fórmula para resolver la ecuación cuadrática, encuentre el raíces enteras o calcular el discriminante.

Pasos

Método 1 de 3: Cómo resolver una ecuación cúbica sin un término constante

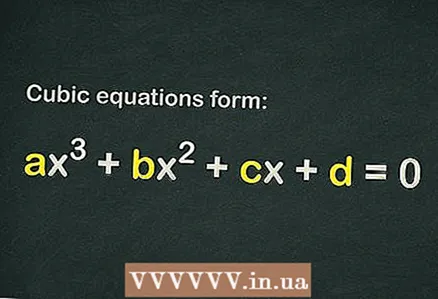1. 1 Averigüe si hay un término libre en la ecuación cúbica. D{ Displaystyle d}. La ecuación cúbica tiene la forma ${ Displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Para que una ecuación se considere cúbica, es suficiente que solo el término ${ Displaystyle x ^ {3}}$ (es decir, puede que no haya otros miembros en absoluto).
   • Si la ecuación tiene un término libre ${ Displaystyle d}$, utilice un método diferente.
   • Si en la ecuación ${ Displaystyle a = 0}$, no es cúbico.
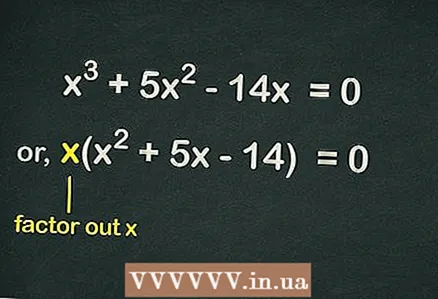2. 2 Sacar de los soportes X{ Displaystyle x}. Dado que no hay un término libre en la ecuación, cada término de la ecuación incluye la variable ${ Displaystyle x}$... Esto significa que uno ${ Displaystyle x}$ puede excluirse de los paréntesis para simplificar la ecuación. Por lo tanto, la ecuación se escribirá así: ${ Displaystyle x (ax ^ {2} + bx + c)}$.
   • Por ejemplo, dada una ecuación cúbica ${ Displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Sacar ${ Displaystyle x}$ corchetes y obtener ${ Displaystyle x (3x ^ {2} -2x + 14) = 0}$
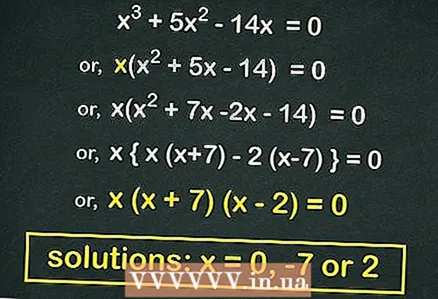3. 3 Factoriza (el producto de dos binomios) la ecuación cuadrática (si es posible). Muchas ecuaciones cuadráticas de la forma ${ Displaystyle ax ^ {2} + bx + c = 0}$ se puede factorizar. Tal ecuación resultará si sacamos ${ Displaystyle x}$ fuera de los corchetes. En nuestro ejemplo:
   • Sacar de los soportes ${ Displaystyle x}$: ${ Displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Factoriza la ecuación cuadrática: ${ Displaystyle x (x + 7) (x-2) = 0}$
   • Equivale cada contenedor a ${ displaystyle 0}$... Las raíces de esta ecuación son ${ Displaystyle x = 0, x = -7, x = 2}$.
4. 4 Resuelve una ecuación cuadrática usando una fórmula especial. Haga esto si la ecuación cuadrática no se puede factorizar. Para encontrar dos raíces de una ecuación, los valores de los coeficientes ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ sustituto en la fórmula ${ Displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • En nuestro ejemplo, sustituya los valores de los coeficientes ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ (${ Displaystyle 3}$, ${ displaystyle -2}$, ${ Displaystyle 14}$) en la fórmula:

     ${ Displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ Displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ Displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ Displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ Displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Primera raíz:

     ${ Displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ Displaystyle { frac {2 + 12,8i} {6}}}$

   • Segunda raíz:

     ${ Displaystyle { frac {2-12,8i} {6}}}$

5. 5 Usa raíces cero y cuadráticas como soluciones para la ecuación cúbica. Las ecuaciones cuadráticas tienen dos raíces, mientras que las cúbicas tienen tres. Ya ha encontrado dos soluciones: estas son las raíces de la ecuación cuadrática. Si coloca "x" fuera de los corchetes, la tercera solución sería ${ displaystyle 0}$.
   • Si sacas "x" de los corchetes, obtienes ${ Displaystyle x (ax ^ {2} + bx + c) = 0}$, es decir, dos factores: ${ Displaystyle x}$ y una ecuación cuadrática entre paréntesis. Si alguno de estos factores es ${ displaystyle 0}$, la ecuación completa también es igual a ${ displaystyle 0}$.
   • Por tanto, dos raíces de una ecuación cuadrática son soluciones de una ecuación cúbica. La tercera solución es ${ Displaystyle x = 0}$.

Método 2 de 3: Cómo encontrar raíces enteras usando multiplicadores

1. 1 Asegúrese de que haya un término libre en la ecuación cúbica D{ Displaystyle d}. Si en una ecuación de la forma ${ Displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ hay un miembro gratis ${ Displaystyle d}$ (que no es igual a cero), no funcionará poner "x" fuera de los corchetes. En este caso, utilice el método descrito en esta sección.
   • Por ejemplo, dada una ecuación cúbica ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Para obtener cero en el lado derecho de la ecuación, agregue ${ Displaystyle 6}$ a ambos lados de la ecuación.
   • La ecuación resultará ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Como ${ Displaystyle d = 6}$, no se puede utilizar el método descrito en la primera sección.
2. 2 Escribe los factores del coeficiente a{ Displaystyle a} y un miembro gratis D{ Displaystyle d}. Es decir, encuentre los factores del número en ${ Displaystyle x ^ {3}}$ y números antes del signo igual. Recuerda que los factores de un número son los números que, cuando se multiplican, producen ese número.
   • Por ejemplo, para obtener el número 6, necesitas multiplicar ${ Displaystyle 6 times 1}$ y ${ Displaystyle 2 times 3}$... Entonces los números 1, 2, 3, 6 son factores del número 6.
   • En nuestra ecuación ${ Displaystyle a = 2}$ y ${ Displaystyle d = 6}$... Multiplicadores 2 son 1 y 2... Multiplicadores 6 son los numeros 1, 2, 3 y 6.
3. 3 Divide cada factor a{ Displaystyle a} para cada factor D{ Displaystyle d}. Como resultado, obtienes muchas fracciones y varios números enteros; las raíces de la ecuación cúbica serán uno de los números enteros o el valor negativo de uno de los números enteros.
   • En nuestro ejemplo, divide los factores ${ Displaystyle a}$ (1 y 2) por factores ${ Displaystyle d}$ (1, 2, 3 y 6). Obtendrás: ${ Displaystyle 1}$, ${ Displaystyle { frac {1} {2}}}$, ${ Displaystyle { frac {1} {3}}}$, ${ Displaystyle { frac {1} {6}}}$, ${ Displaystyle 2}$ y ${ Displaystyle { frac {2} {3}}}$... Ahora agregue valores negativos de las fracciones y números obtenidos a esta lista: ${ Displaystyle 1}$, ${ Displaystyle -1}$, ${ Displaystyle { frac {1} {2}}}$, ${ Displaystyle - { frac {1} {2}}}$, ${ Displaystyle { frac {1} {3}}}$, ${ Displaystyle - { frac {1} {3}}}$, ${ Displaystyle { frac {1} {6}}}$, ${ Displaystyle - { frac {1} {6}}}$, ${ Displaystyle 2}$, ${ displaystyle -2}$, ${ Displaystyle { frac {2} {3}}}$ y ${ Displaystyle - { frac {2} {3}}}$... Las raíces enteras de la ecuación cúbica son algunos números de esta lista.
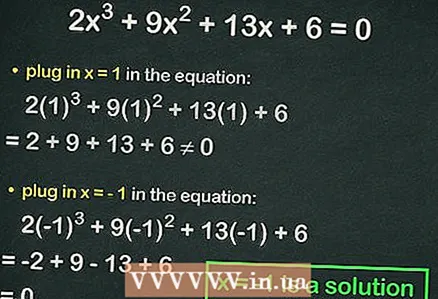4. 4 Inserta números enteros en la ecuación cúbica. Si la igualdad es verdadera, el número sustituido es la raíz de la ecuación. Por ejemplo, sustituya en la ecuación ${ Displaystyle 1}$:
   • ${ Displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ Displaystyle 2 + 9 + 13 + 6}$ ≠ 0, es decir, no se observa igualdad. En este caso, ingrese el siguiente número.
   • Sustituir ${ Displaystyle -1}$: ${ Displaystyle (-2) +9 + (- 13) +6}$ = 0. Por lo tanto, ${ Displaystyle -1}$ es la raíz completa de la ecuación.
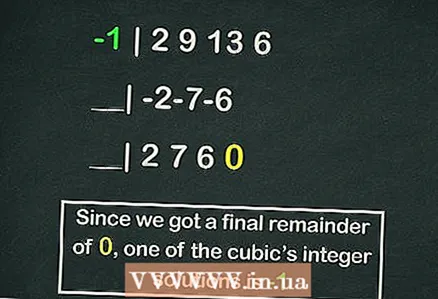5. 5 Usa el método de dividir polinomios por El esquema de Hornerpara encontrar las raíces de la ecuación más rápido. Haga esto si no desea sustituir manualmente números en la ecuación. En el esquema de Horner, los números enteros se dividen por los valores de los coeficientes de la ecuación ${ Displaystyle a}$, ${ Displaystyle b}$, ${ Displaystyle c}$ y ${ Displaystyle d}$... Si los números son divisibles uniformemente (es decir, el resto es ${ displaystyle 0}$), un número entero es la raíz de la ecuación.
   • El esquema de Horner merece un artículo aparte, pero el siguiente es un ejemplo de cómo calcular una de las raíces de nuestra ecuación cúbica usando este esquema:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Entonces el resto es ${ displaystyle 0}$, pero ${ Displaystyle -1}$ es una de las raíces de la ecuación.

Método 3 de 3: Cómo resolver una ecuación usando el discriminante

1. 1 Escribe los valores de los coeficientes de la ecuación. a{ Displaystyle a}, B{ Displaystyle b}, C{ Displaystyle c} y D{ Displaystyle d}. Le recomendamos que anote los valores de los coeficientes indicados con anticipación para no confundirse en el futuro.
   • Por ejemplo, dada la ecuación ${ Displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Anote ${ Displaystyle a = 1}$, ${ Displaystyle b = -3}$, ${ Displaystyle c = 3}$ y ${ Displaystyle d = -1}$... Recuerda que si antes ${ Displaystyle x}$ no hay número, el coeficiente correspondiente todavía existe y es igual a ${ Displaystyle 1}$.
2. 2 Calcule el discriminante cero usando una fórmula especial. Para resolver una ecuación cúbica utilizando el discriminante, debe realizar una serie de cálculos difíciles, pero si realiza todos los pasos correctamente, este método se volverá indispensable para resolver las ecuaciones cúbicas más complejas. Primer cálculo ${ Displaystyle Delta _ {0}}$ (discriminante cero) es el primer valor que necesitamos; para hacer esto, sustituya los valores correspondientes en la fórmula ${ Displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • El discriminante es un número que caracteriza las raíces de un polinomio (por ejemplo, el discriminante de una ecuación cuadrática se calcula mediante la fórmula ${ displaystyle b ^ {2} -4ac}$).
   • En nuestra ecuación:

     ${ Displaystyle b ^ {2} -3ac}$

     ${ Displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ Displaystyle 9-3 (1) (3)}$

     ${ Displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Calcule el primer discriminante usando la fórmula Δ1=2B3−9aBC+27a2D{ Displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Primer discriminante ${ Displaystyle Delta _ {1}}$ - este es el segundo valor importante; para calcularlo, inserte los valores correspondientes en la fórmula especificada.
   • En nuestra ecuación:

     ${ Displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ Displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ Displaystyle -54 + 81-27}$

     ${ Displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Calcular:${ Displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Es decir, encuentre el discriminante de la ecuación cúbica a través de los valores obtenidos ${ Displaystyle Delta _ {0}}$ y ${ Displaystyle Delta _ {1}}$... Si el discriminante de una ecuación cúbica es positivo, la ecuación tiene tres raíces; si el discriminante es cero, la ecuación tiene una o dos raíces; si el discriminante es negativo, la ecuación tiene una raíz.
   • Una ecuación cúbica siempre tiene al menos una raíz, ya que la gráfica de esta ecuación se cruza con el eje X al menos en un punto.
   • En nuestra ecuación ${ Displaystyle Delta _ {0}}$ y ${ Displaystyle Delta _ {1}}$ son iguales ${ displaystyle 0}$, para que puedas calcular fácilmente ${ Displaystyle Delta}$:

     ${ Displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ Displaystyle 0-0 div 27}$

     ${ Displaystyle 0 = Delta}$... Por tanto, nuestra ecuación tiene una o dos raíces.

5. 5 Calcular:${ Displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } right) div 2}}}$. ${ Displaystyle C}$ - esta es la última cantidad importante que se encuentra; te ayudará a calcular las raíces de la ecuación. Sustituye los valores en la fórmula especificada ${ Displaystyle Delta _ {1}}$ y ${ Displaystyle Delta _ {0}}$.
   • En nuestra ecuación:

     ${ Displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ Displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ Displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ Displaystyle 0 = C}$

6. 6 Encuentra tres raíces de la ecuación. Hazlo con la fórmula ${ Displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, donde ${ Displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, pero norte es igual a 1, 2 o 3... Sustituya los valores apropiados en esta fórmula; como resultado, obtendrá tres raíces de la ecuación.
   • Calcule el valor usando la fórmula en norte = 1, 2 o 3y luego verifique la respuesta. Si obtiene 0 cuando verifica su respuesta, este valor es la raíz de la ecuación.
   • En nuestro ejemplo, sustituya 1 en ${ Displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ y obten 0, es decir 1 es una de las raíces de la ecuación.