Contenido

• Pasos
• Método 1 de 3: Parte 1: Determinación del punto de inflexión
• Método 2 de 3: Calcular las derivadas de una función
• Método 3 de 3: Parte 3: Encuentra el punto de inflexión
• Consejos

En cálculo diferencial, un punto de inflexión es un punto en una curva en el que su curvatura cambia de signo (de más a menos o de menos a más). Este concepto se utiliza en ingeniería mecánica, economía y estadística para identificar cambios significativos en los datos.

Pasos

Método 1 de 3: Parte 1: Determinación del punto de inflexión

1. 1 Definición de función cóncava. El medio de cualquier cuerda (un segmento que conecta dos puntos) del gráfico de una función cóncava se encuentra debajo del gráfico o sobre él.
2. 2 Definición de función convexa. El medio de cualquier acorde (un segmento que conecta dos puntos) del gráfico de una función convexa se encuentra sobre el gráfico o sobre él.
3. 3 Determinación de las raíces de la función. La raíz de una función es el valor de la variable "x" en la que y = 0.
   • Al trazar una función, las raíces son los puntos en los que la gráfica cruza el eje x.

Método 2 de 3: Calcular las derivadas de una función

1. 1 Encuentra la primera derivada de la función. Mire las reglas de diferenciación en el libro de texto; tienes que aprender a tomar las primeras derivadas y solo luego pasar a cálculos más complejos. Las primeras derivadas se denominan f '(x). Para expresiones de la forma ax ^ p + bx ^ (p - 1) + cx + d, la primera derivada es: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Por ejemplo, encuentre los puntos de inflexión de la función f (x) = x ^ 3 + 2x -1. La primera derivada de esta función es:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Encuentra la segunda derivada de la función. La segunda derivada es la derivada de la primera derivada de la función original. La segunda derivada se denota como f ′ ′ (x).
   • En el ejemplo anterior, la segunda derivada es:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Establece la segunda derivada en cero y resuelve la ecuación resultante. El resultado será el punto de inflexión esperado.
   • En el ejemplo anterior, su cálculo se ve así:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Encuentra la tercera derivada de la función. Para verificar que su resultado sea en realidad un punto de inflexión, encuentre la tercera derivada, que es la derivada de la segunda derivada de la función original. La tercera derivada se denota como f ′ ′ ′ (x).
   • En el ejemplo anterior, la tercera derivada es:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Método 3 de 3: Parte 3: Encuentra el punto de inflexión

1. 1 Mira la tercera derivada. La regla estándar para estimar un punto de inflexión es que si la tercera derivada no es cero (es decir, f ′ ′ ′ (x) ≠ 0), entonces el punto de inflexión es el verdadero punto de inflexión. Mira la tercera derivada; si no es cero, entonces ha encontrado el punto de inflexión real.
   • En el ejemplo anterior, la tercera derivada es 6, no 0.Entonces has encontrado el verdadero punto de inflexión.
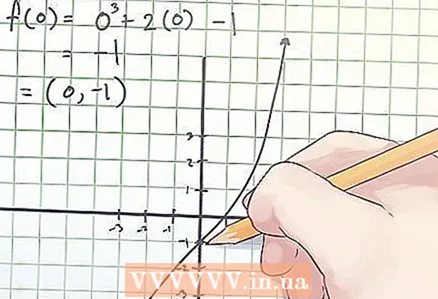2. 2 Encuentra las coordenadas del punto de inflexión. Las coordenadas del punto de inflexión se indican como (x, f (x)), donde x es el valor de la variable independiente "x" en el punto de inflexión, f (x) es el valor de la variable dependiente "y" en la inflexión punto.
   • En el ejemplo anterior, al igualar la segunda derivada a cero, encontró que x = 0. Entonces, para determinar las coordenadas del punto de inflexión, encuentre f (0). Su cálculo se ve así:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
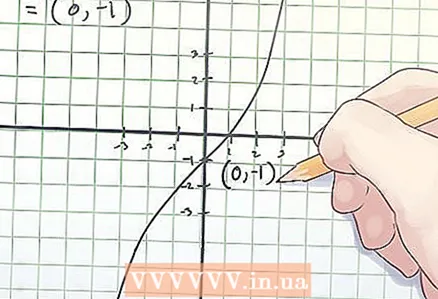3. 3 Escribe las coordenadas del punto de inflexión. Las coordenadas del punto de inflexión son los valores xyf (x) encontrados.
   • En el ejemplo anterior, el punto de inflexión está en las coordenadas (0, -1).

Consejos

• La primera derivada de un término libre (número primo) es siempre cero.