Contenido

• Pasos
• Consejo

Si eres matemático o programador gráfico, probablemente tendrás que encontrar el ángulo entre dos vectores dados. En este artículo, wikiHow te muestra cómo hacer precisamente eso.

Pasos

Parte 1 de 2: Encuentra el ángulo entre dos vectores

1. 

   Definición vectorial. Escribe toda la información sobre los dos vectores que tienes. Suponga que solo tiene los parámetros especificados de sus coordenadas dimensionales (también llamadas componentes). Si ya conoce la longitud (magnitud) de un vector, puede omitir algunos de los pasos siguientes.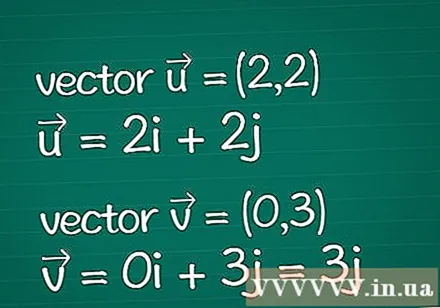
   • Ejemplo: vector bidimensional = (2,2) y vector bidimensional = (0,3). También se pueden escribir como = 2yo + 2j y = 0yo + 3j = 3j.
   • Aunque se utilizan vectores bidimensionales en el ejemplo de este artículo, las siguientes instrucciones pueden aplicarse a vectores con cualquier número de dimensiones.

2. 

   
   
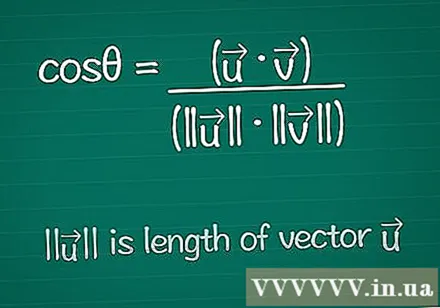
   Escribe la fórmula del coseno. Para encontrar el ángulo θ entre dos vectores, comenzamos con la fórmula para encontrar el coseno de ese ángulo. Puede aprender sobre esta fórmula a continuación, o simplemente escribirla así:
   • cosθ = (•) / (|||| ||||)
   • |||| significa "longitud del vector".
   • • es el producto escalar de los dos vectores; esto se explica a continuación.

3. 

   
   
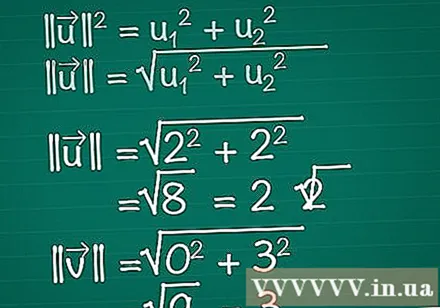
   Calcula la longitud de cada vector. Imagina que un triángulo rectángulo está formado por las componentes x, y del vector y el vector en sí. El vector forma la hipotenusa del triángulo, por lo que para encontrar su longitud usamos el teorema de Pitágoras. De hecho, esta fórmula se puede extender fácilmente a un vector de cualquier número de dimensiones.
   • || u || = u₁ + u₂. Si un vector tiene más de dos elementos, solo necesita seguir agregando + u₃ + u₄ +...
   • Por tanto, para un vector bidimensional, || u || = √ (u₁ + u₂).
   • En este ejemplo, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
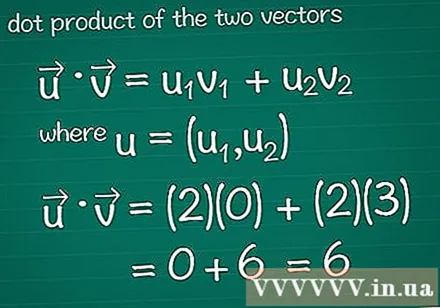
   Calcula el producto escalar de dos vectores. Quizás haya aprendido el método de multiplicación de vectores, también conocido como escalar esta. Para calcular el producto escalar en relación con su composición, multiplique los ingredientes en cada dirección juntos, luego sume el resultado completo.
   • Para el programa de gráficos, consulte Consejos antes de seguir leyendo.
   • En matemáticas • = u₁v₁ + u₂v₂, donde, u = (u₁, u₂). Si el vector tiene más de dos elementos, simplemente agregue + u₃v₃ + u₄v₄...
   • En este ejemplo, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Este es el producto escalar del vector y el vector.

5. 

   Ponga los resultados obtenidos en la fórmula. Recuerda que cosθ = (•) / (|||| || ||). Ahora conocemos tanto el producto escalar como la longitud de cada vector. Ingrese estos en la fórmula para calcular el coseno del ángulo.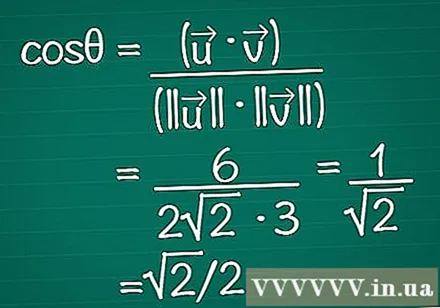
   • En nuestro ejemplo, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Calcula el ángulo según su coseno. Puede usar la función arccos o cos en una calculadora para encontrar θ a partir de un valor de cos conocido. Con algunos resultados, puede encontrar el ángulo basándose en el círculo unitario.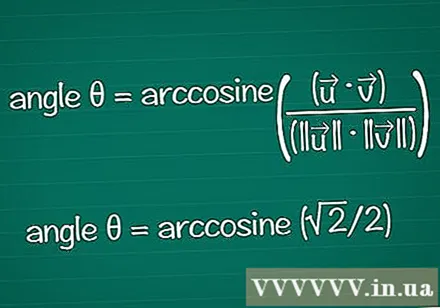
   • En el ejemplo, cosθ = √2 / 2. Ingrese "arccos (√2 ​​/ 2)" en su calculadora para encontrar el ángulo. O puede encontrar el ángulo θ en el círculo unitario, en la posición cosθ = √2 / 2. Es cierto para θ = /₄ o 45º.
   • Combinando todo, la fórmula final es: ángulo θ = arcocoseno ((•) / (|||| || ||))
   anuncio

Parte 2 de 2: Determinación de la fórmula del ángulo

1. 

   Comprende el propósito de la fórmula. Esta fórmula no se derivó de las reglas existentes. En cambio, se forma como la definición del producto escalar y el ángulo entre los dos vectores. Aun así, no fue una decisión arbitraria. Volviendo a la geometría básica, podemos entender por qué esta fórmula proporciona definiciones intuitivas y útiles.
   • Los ejemplos siguientes utilizan vectores bidimensionales porque son los más sencillos y fáciles de entender. Los vectores tridimensionales o más tienen propiedades definidas por fórmulas generales casi similares.

2. 

   Repase el teorema de Coseno. Considere un triángulo ordinario con un ángulo θ entre los lados ayb, lado opuesto c. El teorema del coseno establece que c = a + b -2abporque(θ). Este resultado se extrae simplemente de la geometría básica.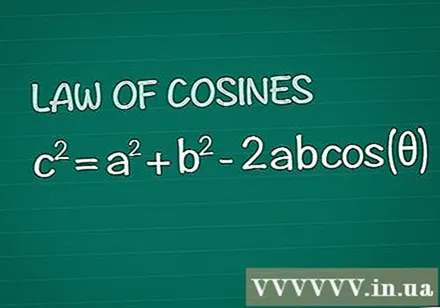

3. 

   Conecta dos vectores, formando un triángulo. Dibuja un par de vectores bidimensionales en papel, vectores y vectores, siendo θ el ángulo entre ellos. Dibuja un tercer vector entre estos dos para crear un triángulo. En otras palabras, dibuja un vector tal que + =. Vector = -.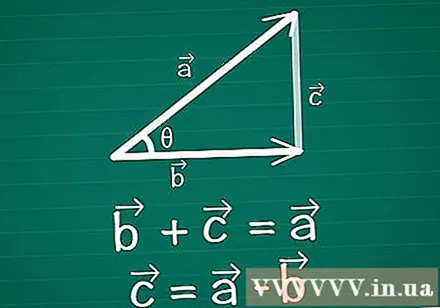

4. 

   Escribe el teorema del coseno para este triángulo. Sustituye la longitud del lado de nuestro "triángulo vectorial" en el teorema del coseno:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||porque(θ)

5. 

   Reescribe con producto escalar. Recuerde, un producto escalar es la imagen de un vector sobre el otro. El producto escalar de un vector consigo mismo no requiere proyección, porque aquí no hay diferencia de dirección. Eso significa • = || a ||. Usando esto, reescribimos la ecuación:
   • (-) • (-) = • + • - 2 || a || || b ||porque(θ)

6. 

   Reescribió con éxito la misma fórmula. Expande el lado izquierdo de la fórmula, luego simplifica para obtener la fórmula utilizada para encontrar ángulos.
   • • - • - • + • = • + • - 2 || a || || b ||porque(θ)
   • - • - • = -2 || a || || b ||porque(θ)
   • -2 (•) = -2 || a || || b ||porque(θ)
   • • = || a || || b ||porque(θ)
   anuncio

Consejo

• Para cambiar valores y resolver el problema rápidamente, use esta fórmula para cualquier par de vectores bidimensionales: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Si está trabajando con software de gráficos por computadora, es probable que solo tenga que preocuparse por la dimensión de los vectores sin preocuparse por su longitud. Utilice los siguientes pasos para acortar una ecuación y acelerar su programa:
  • Normalice cada vector para que sean iguales a 1. Para hacer esto, divida cada uno de los componentes del vector por su longitud.
  • Obtenga el producto normalizado del escalar en lugar del vector original.
  • Dado que la longitud es 1, podemos excluir los elementos de longitud de la ecuación. Finalmente, la ecuación de ángulo obtenida es arccos (•).
• Con base en la fórmula del coseno, podemos determinar rápidamente si el ángulo es agudo u obtuso. Comience con cosθ = (•) / (|||| ||||):
  • Los lados izquierdo y derecho de la ecuación deben tener el mismo signo (positivo o negativo).
  • Dado que la longitud es siempre positiva, cosθ debe tener el mismo signo que el producto escalar.
  • Por tanto, si el producto es positivo, cosθ también es positivo. Estamos en el primer cuadrante del círculo unitario, con θ <π / 2 o 90º. El ángulo a encontrar es el ángulo agudo.
  • Si el producto escalar es negativo, cosθ es negativo. Estamos en el segundo cuadrante del círculo unitario, con π / 2 <θ ≤ π o 90º <θ ≤ 180º. Ese es el rincón de la prisión.