Contenido

• Pasos
• Consejo

La varianza mide la dispersión del conjunto de datos. Es muy útil para construir modelos estadísticos: una baja varianza puede ser una indicación de que está describiendo un error aleatorio o ruido en lugar de la relación subyacente en los datos. Con este artículo, wikiHow te enseñará cómo calcular la varianza.

Pasos

Método 1 de 2: calcular la varianza de una muestra

1. 

   Escriba su conjunto de datos de muestra. En la mayoría de los casos, los estadísticos solo tienen información sobre una muestra o subconjunto de la población que están estudiando. Por ejemplo, en lugar de hacer un análisis general del "costo de cada automóvil en Alemania", un estadístico podría encontrar el costo de una muestra aleatoria de unos pocos miles de automóviles. Ese estadístico puede usar esta muestra para obtener una buena estimación del costo de un automóvil en Alemania. Sin embargo, es más probable que no coincida exactamente con los números reales.
   • Por ejemplo: Al analizar la cantidad de muffins vendidos por día en una cafetería, tomó una muestra aleatoria de seis días y obtuvo los siguientes resultados: 38, 37, 36, 28, 18, 14, 12, 11, 10,7, 9,9. Esta es una muestra, no una población, porque no tiene datos para todos los días que la tienda está abierta.
   • Si cada Puntos de datos en el maestro, vaya al método a continuación.

2. 

   
   
   Anote la fórmula de varianza de la muestra. La varianza de un conjunto de datos indica el grado de dispersión de los puntos de datos. Cuanto más cerca de cero esté la varianza, más cerca se agruparán los puntos de datos. Cuando trabaje con conjuntos de datos de muestra, utilice la siguiente fórmula para calcular la varianza:
   • = /_{(n - 1)}
   • es la varianza. La varianza siempre se calcula en unidades cuadradas.
   • representa un valor en su conjunto de datos.
   • ∑, que significa "suma", le indica que debe calcular los siguientes parámetros para cada valor y luego sumarlos.
   • x̅ es la media de la muestra.
   • n es el número de puntos de datos.

3. 

   
   
   Calcule la media de la muestra. El símbolo x̅ o "x-horizontal" se utiliza para indicar la media de la muestra. Calcule como lo haría con cualquier promedio: sume todos los puntos de datos y divídalos por el número de puntos.
   • Por ejemplo: Primero, sume sus puntos de datos: 17 + 15 + 23 + 7 + 9 + 13 = 84
     A continuación, divida el resultado por el número de puntos de datos, en este caso seis: 84 ÷ 6 = 14.
     Media muestral = x̅ = 14.
   • Puede pensar en la media como el "punto central" de los datos. Si los datos se centran en la media, la varianza es baja. Si están dispersos lejos de la media, la varianza es alta.

4. 

   
   
   Reste la media de cada punto de datos. Ahora es el momento de calcular - x̅, donde se encuentra cada punto de su conjunto de datos. Cada resultado indicará la desviación de la media de cada punto correspondiente, o para decirlo simplemente, la distancia de este a la media.
   • Por ejemplo:
     - x̅ = 17 - 14 = 3
     - x̅ = 15 - 14 = 1
     - x̅ = 23 - 14 = 9
     - x̅ = 7 - 14 = -7
     - x̅ = 9 - 14 = -5
     - x̅ = 13 - 14 = -1
   • Es muy fácil verificar tus cálculos, porque los resultados deben sumar cero, esto se debe a que, por la media de la media, los resultados negativos (la distancia de la media a los números pequeños). los resultados positivos (distancia de la media a números mayores) se eliminan por completo.

5. 

   Cuadre todos los resultados. Como se señaló anteriormente, la lista de desviaciones actuales (- x̅) tiene una suma de cero. Eso significa que la "desviación promedio" también será siempre cero y no se puede decir nada sobre la dispersión de los datos. Para resolver este problema, encontramos el cuadrado de cada desviación. Gracias a eso, todos son números positivos, los valores negativos y los valores positivos ya no se cancelan entre sí y dan la suma cero.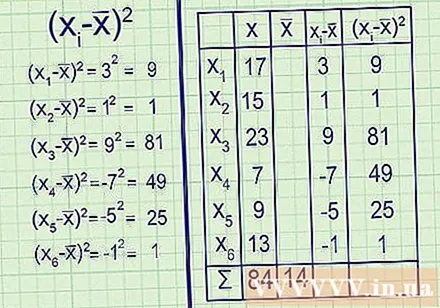
   • Por ejemplo:
     (- X)
     - X)
     9 = 81
     (-7) = 49
     (-5) = 25
     (-1) = 1
   • Ahora tiene (- x̅) para cada punto de datos de la muestra.

6. 

   Calcula la suma de los valores al cuadrado. Ahora es el momento de calcular el numerador completo de la fórmula: ∑. El ciclo grande, ∑, requiere que agregue el siguiente valor de elemento para cada valor. Ha calculado (- x̅) para cada valor de la muestra, por lo que todo lo que tiene que hacer es sumar los resultados.
   • Por ejemplo: 9 + 1 + 81 + 49 + 25 + 1 = 166.

7. 

   Dividir por n - 1, donde n es el número de puntos de datos. Hace mucho tiempo, al calcular la varianza de la muestra, los estadísticos solo dividían entre n. Esa división le dará la media de la desviación al cuadrado, que coincide exactamente con la varianza de esa muestra. Sin embargo, tenga en cuenta que la muestra es solo una estimación de una población más grande. Si toma otra muestra aleatoria y hace el mismo cálculo, obtendrá un resultado diferente. Resulta que dividir por n -1 en lugar de n le da una mejor estimación de la varianza de una población más grande, lo que realmente le importa. Esta corrección es tan común que ahora es la definición aceptada de varianza muestral.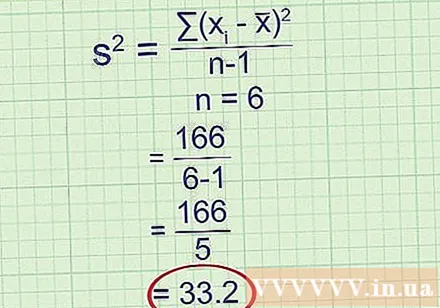
   • Por ejemplo: Hay seis puntos de datos en la muestra, entonces n = 6.
     Varianza de la muestra = 33,2

8. 

   Comprender la varianza y la desviación estándar. Tenga en cuenta que, dado que hay potencias en la fórmula, la varianza se mide en el cuadrado de las unidades de los datos originales. Esto es visualmente confuso. En cambio, a menudo la desviación estándar es bastante útil. Pero no tiene sentido desperdiciar ningún esfuerzo, ya que la desviación estándar está determinada por la raíz cuadrada de la varianza. Es por eso que la varianza de la muestra se escribe en términos y la desviación estándar de una muestra es.
   • Por ejemplo, la desviación estándar de la muestra anterior = s = √33.2 = 5.76.
   anuncio

Método 2 de 2: calcular la varianza de una población

1. 

   Comenzando con el conjunto de datos maestros. El término "población" se utiliza para referirse a todas las observaciones relevantes. Por ejemplo, si está investigando la edad de los residentes de Hanoi, su población general incluirá las edades de todas las personas que viven en Hanoi. Por lo general, crearía una hoja de cálculo para un conjunto de datos grande como este, pero aquí hay un conjunto de datos de ejemplo más pequeño:
   • Por ejemplo: En la habitación de un acuario, hay exactamente seis acuarios. Estos seis tanques contienen la siguiente cantidad de peces:
     
     
     
     
     
     

2. 

   Escriba la fórmula para la varianza general. Dado que una población contiene todos los datos que necesitamos, esta fórmula nos da la varianza exacta de la población. Para distinguirlo de la varianza de la muestra (que es solo una estimación), los estadísticos usan otras variables:
   • σ = /_norte
   • σ = varianza de la muestra. Esta es la salchicha normalmente cuadriculada. La varianza se mide en unidades cuadradas.
   • representa un elemento en su conjunto de datos.
   • El elemento en ∑ se calcula para cada valor y luego se suma.
   • μ es la media general.
   • n es el número de puntos de datos en la población.

3. 

   Calcula la media de la población. Al analizar una población, el símbolo μ ("mu") representa la media aritmética. Para encontrar la media, sume todos los puntos de datos, luego divida por el número de puntos.
   • Puede pensar en la media como "promedio", pero tenga cuidado, porque la palabra tiene muchas definiciones matemáticas.
   • Por ejemplo: valor medio = μ = = 10,5

4. 

   Reste la media de cada punto de datos. Los puntos de datos más cercanos a la media tienen una diferencia más cercana a cero. Repita el problema de la resta para todos los puntos de datos y probablemente comenzará a sentir la dispersión de los datos.
   • Por ejemplo:
     - μ = 5 – 10,5 = -5,5
     - μ = 5 – 10,5 = -5,5
     - μ = 8 – 10,5 = -2,5
     - μ = 12 - 10., = 1,5
     - μ = 15 – 10,5 = 4,5
     - μ = 18 – 10,5 = 7,5

5. 

   Cuadre cada signo. En este punto, algunos de los resultados obtenidos en el paso anterior serán negativos y algunos serán positivos.Si visualiza los datos en una línea isomórfica, estos dos elementos representan los números a la izquierda y derecha de la media. Esto no sería útil para calcular la varianza, ya que estos dos grupos se cancelarían entre sí. En su lugar, cuadre todos para que sean positivos.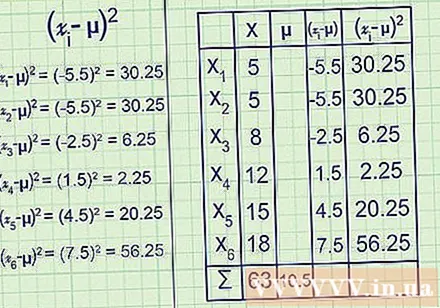
   • Por ejemplo:
     (- μ) para cada valor de yo va de 1 a 6:
     (-5,5) = 30,25
     (-5,5) = 30,25
     (-2,5) = 6,25
     (1,5) = 2,25
     (4,5) = 20,25
     (7,5) = 56,25

6. 

   Encuentra el promedio de tus resultados. Ahora tiene un valor para cada punto de datos, relacionado (no directamente) con qué tan lejos está ese punto de datos de la media. Promedio sumándolos y dividiendo por la cantidad de valores que tienes.
   • Por ejemplo:
     Varianza general = 24,25

7. 

   Receta de contacto. Si no está seguro de cómo se ajusta esto a la fórmula descrita al principio del método, escriba todo el problema a mano y no abrevie: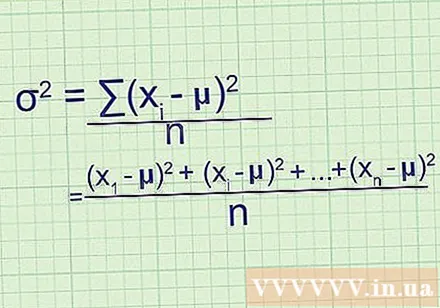
   • Después de encontrar la diferencia de la media y elevar al cuadrado, obtiene (- μ), (- μ), y así sucesivamente hasta (- μ), donde está el punto de datos final. en el conjunto de datos.
   • Para encontrar el promedio de estos valores, súmelos y divídalos por n: ((- μ) + (- μ) + ... + (- μ)) / n
   • Después de reescribir el numerador con notación sigmoidea, tiene /_norte, varianza de la fórmula.
   anuncio

Consejo

• Dado que la varianza es difícil de interpretar, este valor a menudo se calcula como el punto de partida para encontrar la desviación estándar.
• El uso de "n-1" en lugar de "n" en el denominador es una técnica llamada corrección de Bessel. La muestra es solo una estimación de una población completa y la media de la muestra tiene un cierto sesgo para coincidir con esa estimación. Esta corrección elimina el sesgo anterior. Se refiere al hecho de que una vez que se han enumerado n - 1 puntos de datos, el último punto norte fue una constante, porque solo se usaron ciertos valores para calcular la media de la muestra (x̅) en la fórmula de varianza.