Contenido

• Al paso
• Parte 1 de 4: Elaboración de la matriz
• Parte 2 de 4: Aprender las operaciones para resolver un sistema con una matriz
• Parte 3 de 4: fusiona los pasos para resolver la galaxia
• Parte 4 de 4: Verifica tu solución
• Consejos

Una matriz es una forma muy útil de representar números en un formato de bloque, que luego puede usar para resolver un sistema de ecuaciones lineales. Si solo tiene dos variables, es probable que utilice un método diferente. Lea sobre esto en Resolver un sistema de ecuaciones para ver ejemplos de estos otros métodos. Pero si tiene tres o más variables, una matriz es ideal. Mediante el uso de combinaciones repetidas de multiplicación y suma, puede llegar sistemáticamente a una solución.

Al paso

Parte 1 de 4: Elaboración de la matriz

1. Verifique que tenga suficientes datos. Para obtener una solución única para cada variable en un sistema lineal usando una matriz, necesita tener tantas ecuaciones como la cantidad de variables que está tratando de resolver. Por ejemplo: con las variables x, y y z necesitas tres ecuaciones. Si tiene cuatro variables, necesita cuatro ecuaciones.
   • Si tiene menos ecuaciones que la cantidad de variables, encontrará algunos límites de las variables (como x = 3y e y = 2z), pero no puede obtener una solución precisa. Para este artículo, solo trabajaremos para encontrar una solución única.
2. Escribe tus ecuaciones en la forma estándar. Antes de poder poner los datos de las ecuaciones en forma de matriz, primero escribe cada ecuación en forma estándar. La forma estándar de una ecuación lineal es Ax + By + Cz = D, donde las letras mayúsculas son los coeficientes (números) y el último número (D en este ejemplo) está a la derecha del signo igual.
   • Si tiene más variables, simplemente continúe la línea todo el tiempo que necesite. Por ejemplo, si estuviera intentando resolver un sistema con seis variables, su forma predeterminada sería Au + Bv + Cw + Dx + Ey + Fz = G. En este artículo nos centraremos en sistemas con solo tres variables. Resolver una galaxia más grande es exactamente lo mismo, pero solo requiere más tiempo y más pasos.
   • Tenga en cuenta que en la forma estándar, las operaciones entre los términos son siempre una suma. Si hay una resta en su ecuación, en lugar de una suma, tendrá que trabajar con esto más adelante haciendo que su coeficiente sea negativo. Para que esto sea más fácil de recordar, puede reescribir la ecuación y sumar la operación y hacer que el coeficiente sea negativo. Por ejemplo, puede reescribir la ecuación 3x-2y + 4z = 1 como 3x + (- 2y) + 4z = 1.
3. Coloca los números del sistema de ecuaciones en una matriz. Una matriz es un conjunto de números, dispuestos en una especie de tabla, con los que trabajaremos para resolver el sistema. Básicamente contiene los mismos datos que las ecuaciones en sí, pero en un formato más simple. Para hacer la matriz de sus ecuaciones en forma estándar, simplemente copie los coeficientes y el resultado de cada ecuación en una sola fila y apile esas filas una encima de la otra.
   • Suponga que tiene un sistema que consta de tres ecuaciones 3x + y-z = 9, 2x-2y + z = -3 y x + y + z = 7. La fila superior de su matriz contendrá los números 3, 1, -1, 9, ya que estos son los coeficientes y la solución de la primera ecuación. Tenga en cuenta que se supone que cualquier variable que no tenga un coeficiente tiene un coeficiente de 1. La segunda fila de la matriz se convierte en 2, -2, 1, -3 y la tercera fila se convierte en 1, 1, 1, 7.
   • Asegúrese de alinear los coeficientes x en la primera columna, los coeficientes y en la segunda, los coeficientes z en la tercera y los términos de solución en la cuarta. Cuando haya terminado de trabajar con la matriz, estas columnas serán importantes al escribir su solución.
4. Dibuja un corchete grande alrededor de toda tu matriz. Por convención, una matriz se indica mediante un par de corchetes, [], alrededor de todo el bloque de números. Los corchetes no afectan la solución de ninguna manera, pero indican que está trabajando con matrices. Una matriz puede constar de cualquier número de filas y columnas. En este artículo, usaremos paréntesis alrededor de los términos en una fila para indicar que pertenecen juntos.
5. Uso de simbolismo común. Cuando se trabaja con matrices, es común referirse a las filas con la abreviatura R y las columnas con la abreviatura C. Puede usar números junto con estas letras para indicar una fila o columna específica. Por ejemplo, para indicar la fila 1 de una matriz, puede escribir R1. La fila 2 luego se convierte en R2.
   • Puede indicar cualquier posición específica en una matriz usando una combinación de R y C. Por ejemplo, para indicar un término en la segunda fila, tercera columna, podría llamarlo R2C3.

Parte 2 de 4: Aprender las operaciones para resolver un sistema con una matriz

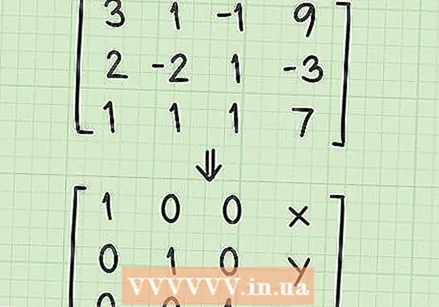1. Comprende la forma de la matriz de solución. Antes de comenzar a resolver su sistema de ecuaciones, debe comprender lo que va a hacer con la matriz. En este punto, tiene una matriz que se ve así:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • Trabaja con una serie de operaciones básicas para crear la "matriz de solución". La matriz de la solución se verá así:
   • 1 0 0 x
   • 0 1 0 años
   • 0 0 1 z
   • Tenga en cuenta que la matriz consta de unos en una línea diagonal con ceros en todos los demás espacios excepto en la cuarta columna. Los números de la cuarta columna son la solución de las variables x, y y z.
2. Usa la multiplicación escalar. La primera herramienta a su disposición para resolver un sistema usando una matriz es la multiplicación escalar. Este es simplemente un término que significa que multiplica los elementos en una fila de la matriz por un número constante (no una variable). Cuando utilice la multiplicación escalar, tenga en cuenta que debe multiplicar cada término de toda la fila por el número que seleccione. Si olvida el primer término y simplemente lo multiplica, obtendrá la solución incorrecta. Sin embargo, no es necesario multiplicar toda la matriz al mismo tiempo. En la multiplicación escalar, solo trabaja en una fila a la vez.
   • Es común usar fracciones en la multiplicación escalar porque a menudo desea obtener una fila diagonal de unos. Acostúmbrate a trabajar con fracciones. También será más fácil (para la mayoría de los pasos para resolver la matriz) poder escribir sus fracciones en forma incorrecta y luego convertirlas nuevamente en números mixtos para la solución final. Por lo tanto, es más fácil trabajar con el número 1 2/3 si lo escribe como 5/3.
   • Por ejemplo, la primera fila (R1) de nuestro problema de ejemplo comienza con los términos [3,1, -1,9]. La matriz de solución debe contener un 1 en la primera posición de la primera fila. Para "cambiar" el 3 a 1, podemos multiplicar toda la fila por 1/3. Esto crea el nuevo R1 de [1,1 / 3, -1 / 3,3].
   • Asegúrese de dejar cualquier signo negativo en su lugar.
3. Utilice la suma de filas o la resta de filas. La segunda herramienta que puede utilizar es sumar o restar dos filas de la matriz. Para crear los términos 0 en su matriz de solución, debe sumar o restar números para llegar al 0. Por ejemplo, si R1 es de una matriz [1,4,3,2] y R2 es [1,3,5,8], entonces puede restar la primera fila de la segunda fila y crear una nueva fila [0, -1, 2.6], porque 1-1 = 0 (primera columna), 3-4 = -1 (segunda columna), 5-3 = 2 (tercera columna) y 8-2 = 6 (cuarta columna). Al realizar una suma o resta de filas, vuelva a escribir su nuevo resultado en lugar de la fila con la que comenzó. En este caso, extraeríamos la fila 2 e insertaríamos la nueva fila [0, -1,2,6].
   • Puede utilizar una notación abreviada y declarar esta acción como R2-R1 = [0, -1,2,6].
   • Recuerde que la suma y la resta son formas opuestas de la misma operación. Piense en ello como sumar dos números o restar lo contrario. Por ejemplo, si comienza con la ecuación simple 3-3 = 0, puede pensar en esto como un problema de suma de 3 + (- 3) = 0. El resultado es el mismo. Esto parece simple, pero a veces es más fácil considerar un problema de una forma u otra. Solo mantén un ojo en tus signos negativos.
4. Combine la suma de filas y la multiplicación escalar en un solo paso. No puede esperar que los términos siempre coincidan, por lo que puede usar una simple suma o resta para crear ceros en su matriz. Más a menudo tendrá que sumar (o restar) un múltiplo de otra fila. Para hacer esto, primero haga la multiplicación escalar, luego agregue ese resultado a la fila de destino que está tratando de cambiar.
   • Suponer; que hay una fila 1 de [1,1,2,6] y una fila 2 de [2,3,1,1]. Quieres un término 0 en la primera columna de R2. Es decir, desea cambiar el 2 a 0. Para hacer esto, debe restar un 2. Puede obtener un 2 multiplicando primero la fila 1 por la multiplicación escalar 2 y luego restando la primera fila de la segunda fila. En forma abreviada, esto se puede escribir como R2-2 * R1. Primero, multiplique R1 por 2 para obtener [2, 2, 4, 12]. Luego reste esto de R2 para obtener [(2-2), (3-2), (1-4), (1-12)]. Simplifique esto y su nuevo R2 será [0,1, -3, -11].
5. Copie las filas que permanecen sin cambios mientras trabaja. A medida que trabaja en la matriz, cambiará una sola fila a la vez, ya sea mediante multiplicación escalar, suma o resta de filas, o una combinación de pasos. Cuando cambie una fila, asegúrese de copiar las otras filas de su matriz en su forma original.
   • Se produce un error común al realizar un paso combinado de multiplicación y suma en un solo movimiento. Por ejemplo, digamos que necesita restar R1 de R2 dos veces. Cuando multiplique R1 por 2 para realizar este paso, recuerde que R1 no cambia en la matriz. Solo haces la multiplicación para cambiar R2. Primero copie R1 en su forma original, luego haga el cambio a R2.
6. Primero trabajar de arriba a abajo. Para resolver el sistema, trabaja en un patrón muy organizado, esencialmente "resolviendo" un término de la matriz a la vez. La secuencia para una matriz de tres variables se verá así:
   • 1. Haga un 1 en la primera fila, primera columna (R1C1).
   • 2. Haga un 0 en la segunda fila, primera columna (R2C1).
   • 3. Haga un 1 en la segunda fila, segunda columna (R2C2).
   • 4. Haga un 0 en la tercera fila, primera columna (R3C1).
   • 5. Haga un 0 en la tercera fila, segunda columna (R3C2).
   • 6. Haga un 1 en la tercera fila, tercera columna (R3C3).
7. Trabaja de abajo hacia arriba. En este punto, si siguió los pasos correctamente, estará a la mitad de la solución. Debe tener la línea diagonal de unos, con ceros debajo. Los números de la cuarta columna no importan en este momento. Ahora vuelve al principio de la siguiente manera:
   • Cree un 0 en la segunda fila, tercera columna (R2C3).
   • Cree un 0 en la primera fila, tercera columna (R1C3).
   • Cree un 0 en la primera fila, segunda columna (R1C2).
8. Compruebe si ha creado la matriz de solución. Si su trabajo es correcto, ha creado la matriz de solución con unos en una línea diagonal de R1C1, R2C2, R3C3 y ceros en las otras posiciones de las tres primeras columnas. Los números de la cuarta columna son las soluciones para su sistema lineal.

Parte 3 de 4: fusiona los pasos para resolver la galaxia

1. Comience con un sistema de ejemplo de ecuaciones lineales. Para practicar estos pasos, comencemos con el sistema que usamos anteriormente: 3x + y-z = 9, 2x-2y + z = -3 y x + y + z = 7. Si escribe esto en una matriz, tiene R1 = [3,1, -1,9], R2 = [2, -2,1, -3] y R3 = [1,1,1,7].
2. Cree un 1 en la primera posición R1C1. Tenga en cuenta que R1 comienza en este punto con un 3. Debe cambiarlo a un 1. Puede hacer esto mediante la multiplicación escalar, multiplicando los cuatro términos de R1 por 1/3. De forma abreviada, puede escribir como R1 * 1/3. Esto da un nuevo resultado para R1 si R1 = [1,1 / 3, -1 / 3,3]. Copie R2 y R2, sin cambios, cuando R2 = [2, -2,1, -3] y R3 = [1,1,1,7].
   • Tenga en cuenta que la multiplicación y la división son solo funciones inversas entre sí. Podemos decir que multiplicamos por 1/3 o dividimos por 3, sin cambiar el resultado.
3. Cree un 0 en la segunda fila, primera columna (R2C1). En este punto, R2 = [2, -2,1, -3]. Para acercarse a la matriz de solución, necesita cambiar el primer término de un 2 a un 0. Puede hacerlo restando el doble del valor de R1, ya que R1 comienza con un 1. En forma abreviada, la operación R2- 2 * R1. Recuerde, no cambia R1, simplemente trabaje con él. Entonces, primero copie R1 si R1 = [1,1 / 3, -1 / 3,3]. Entonces, si duplicas cada término de R1, obtienes 2 * R1 = [2,2 / 3, -2 / 3,6]. Finalmente, reste este resultado del R2 original para obtener su nuevo R2. Trabajando término por término, esta resta se convierte en (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). Los simplificamos al nuevo R2 = [0, -8 / 3,5 / 3, -9]. Tenga en cuenta que el primer término es 0 (cualquiera que sea su objetivo).
   • Escriba la fila 3 (que no ha cambiado) como R3 = [1,1,1,7].
   • Tenga cuidado al restar números negativos para asegurarse de que los signos se mantengan correctos.
   • Ahora primero dejemos las fracciones en su forma incorrecta. Esto facilita los pasos posteriores de la solución. Puedes simplificar las fracciones en el último paso del problema.
4. Cree un 1 en la segunda fila, segunda columna (R2C2). Para seguir formando la línea diagonal de unos, debes convertir el segundo término -8/3 en 1. Haga esto multiplicando toda la fila por el recíproco de ese número (-3/8). Simbólicamente, este paso es R2 * (- 3/8). La segunda fila resultante es R2 = [0,1, -5 / 8,27 / 8].
   • Tenga en cuenta que si la mitad izquierda de la fila comienza a parecerse a la solución con el 0 y el 1, la mitad derecha puede comenzar a verse fea, con fracciones impropias. Déjalos por lo que son por ahora.
   • No olvide seguir copiando las filas intactas, por lo que R1 = [1,1 / 3, -1 / 3,3] y R3 = [1,1,1,7].
5. Cree un 0 en la tercera fila, primera columna (R3C1). Su enfoque ahora se mueve a la tercera fila, R3 = [1,1,1,7]. Para hacer un 0 en la primera posición, debe restar un 1 del 1 que se encuentra actualmente en esa posición. Si mira hacia arriba, hay un 1 en la primera posición de R1. Entonces, solo necesita restar R1 de R3 para obtener el resultado que necesita. Término de trabajo por término, esto se convierte en (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Estos cuatro mini-problemas pueden luego simplificarse al nuevo R3 = [0.2 / 3.4 / 3.4].
   • Continúe copiando a lo largo de R1 = [1.1 / 3, -1 / 3.3] y R2 = [0.1, -5 / 8.27 / 8]. Recuerde que solo cambia una fila a la vez.
6. Haga un 0 en la tercera fila, segunda columna (R3C2). Este valor es actualmente 2/3, pero debe convertirse a 0. A primera vista, parece que puede restar los valores de R1 al doble, ya que la columna correspondiente de R1 contiene 1/3. Sin embargo, si duplica y resta todos los valores de R1, el 0 en la primera columna de R3 cambia, lo que no desea. Este sería un paso atrás en su solución. Entonces tienes que trabajar con alguna combinación de R2. Restar 2/3 de R2 crea un 0 en la segunda columna, sin cambiar la primera columna. En resumen, esto es R3-2 / 3 * R2. Los términos individuales se convierten en (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . Entonces, la simplificación da R3 = [0,0,42 / 24,42 / 24].
7. Cree un 1 en la tercera fila, tercera columna (R3C3). Esta es una simple multiplicación por el recíproco del número que dice. El valor actual es 42/24, por lo que puede multiplicar por 24/42 para obtener el valor que desea 1. Tenga en cuenta que los dos primeros términos son ambos 0, por lo que cualquier multiplicación sigue siendo 0. El nuevo valor de R3 = [0,0,1,1].
   • Tenga en cuenta que las fracciones que parecían bastante complicadas en el paso anterior ya están comenzando a resolverse.
   • Continúe con R1 = [1.1 / 3, -1 / 3.3] y R2 = [0.1, -5 / 8.27 / 8].
   • Tenga en cuenta que en este punto tiene la diagonal de unos para su matriz de solución. Solo tiene que convertir tres elementos de la matriz en ceros para encontrar su solución.
8. Crea un 0 en la segunda fila, tercera columna. R2 es actualmente [0.1, -5 / 8.27 / 8], con un valor de -5/8 en la tercera columna. Tienes que transformarlo a 0. Esto significa que tienes que realizar alguna operación con R3 que consiste en sumar 5/8. Dado que la tercera columna correspondiente de R3 es un 1, debe multiplicar todos los valores de R3 por 5/8 y sumar el resultado a R2. En resumen, esto es R2 + 5/8 * R3. Término para el término esto es R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Esto se puede simplificar a R2 = [0,1,0,4].
   • Luego copie R1 = [1,1 / 3, -1 / 3,3] y R3 = [0,0,1,1].
9. Cree un 0 en la primera fila, tercera columna (R1C3). La primera fila es actualmente R1 = [1,1 / 3, -1 / 3,3]. Tienes que convertir el -1/3 en la tercera columna a un 0, usando alguna combinación de R3. No desea usar R2, porque el 1 en la segunda columna de R2 cambiaría R1 de manera incorrecta. Entonces multiplica R3 * 1/3 y suma el resultado a R1. La notación para esto es R1 + 1/3 * R3. El término para la elaboración de términos resulta en R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Puede simplificar esto a un nuevo R1 = [1,1 / 3,0,10 / 3].
   • Copie el R2 = [0,1,0,4] sin cambios y R3 = [0,0,1,1].
10. Haga un 0 en la primera fila, segunda columna (R1C2). Si todo se hace correctamente, este debería ser el último paso. Tienes que convertir 1/3 en la segunda columna a 0. Puedes obtener esto multiplicando y restando R2 * 1/3. Brevemente, este es R1-1 / 3 * R2. El resultado es R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). Simplificando entonces da R1 = [1,0,0,2].
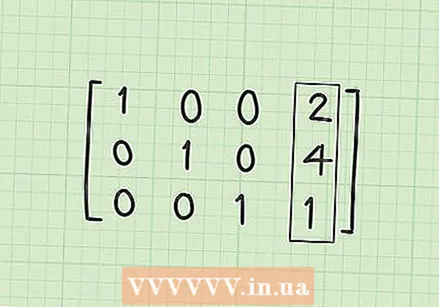11. Busque la matriz de solución. En este punto, si todo salió bien, tendría las tres filas R1 = [1,0,0,2], R2 = [0,1,0,4] y R3 = [0,0,1,1] Tienes que tener. Tenga en cuenta que si escribe esto en la forma de matriz de bloques con las filas una encima de la otra, tiene diagonales unos con ceros más allá, y sus soluciones están en la cuarta columna. La matriz de la solución debería verse así:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Entendiendo su solución. Después de convertir las ecuaciones lineales en una matriz, coloque los coeficientes x en la primera columna, los coeficientes y en la segunda columna, los coeficientes z en la tercera columna. Si desea volver a escribir la matriz en ecuaciones, estas tres líneas de la matriz en realidad significan las tres ecuaciones 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 y 0x + 0y + 1z = 1. Como podemos tachar los términos 0 y no tener que escribir los coeficientes 1, estas tres ecuaciones se simplifican a la solución, x = 2, y = 4 y z = 1. Esta es la solución a su sistema de ecuaciones lineales.

Parte 4 de 4: Verifica tu solución

1. Incluya las soluciones en cada variable en cada ecuación. Siempre es una buena idea comprobar que su solución sea realmente correcta. Haz esto probando tus resultados en las ecuaciones originales.
   • Las ecuaciones originales para este problema eran: 3x + y-z = 9, 2x-2y + z = -3 y x + y + z = 7. Cuando reemplaza las variables con sus valores que encontró, obtiene 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 y 2 + 4 + 1 = 7.
2. Simplifique cualquier comparación. Realice las operaciones en cada ecuación de acuerdo con las reglas básicas de las operaciones. La primera ecuación se simplifica a 6 + 4-1 = 9, o 9 = 9. La segunda ecuación se puede simplificar a 4-8 + 1 = -3 o -3 = -3. La última ecuación es simplemente 7 = 7.
   • Dado que cualquier ecuación se simplifica a un enunciado matemático verdadero, sus soluciones son correctas. Si alguna de las soluciones es incorrecta, revise su trabajo nuevamente y busque cualquier error. Algunos errores comunes ocurren al deshacerse de los signos menos en el camino o confundir la multiplicación y la suma de fracciones.
3. Escriba sus soluciones finales. Para este problema dado, la solución final es x = 2, y = 4 yz = 1.

Consejos

• Si su sistema de ecuaciones es muy complejo, con muchas variables, es posible que pueda usar una calculadora gráfica en lugar de hacer el trabajo a mano. Para obtener información sobre esto, también puede consultar wikiHow.