Contenido

• Al paso

Una ecuación trigonométrica es una ecuación con una o más funciones trigonométricas de la curva trigonométrica variable x. Resolver para x significa encontrar los valores de las curvas trigonométricas cuyas funciones trigonométricas hacen que la ecuación trigonométrica sea verdadera.

• Las respuestas, o valores, de las curvas solución se expresan en grados o radianes. Ejemplos:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 grados; x = 37,12 grados; x = 178,37 grados

• Nota: En el círculo unitario, las funciones trigonométricas de cualquier curva son iguales a las funciones trigonométricas del ángulo correspondiente. El círculo unitario define todas las funciones trigonométricas de la curva variable x. También se usa como prueba para resolver ecuaciones y desigualdades trigonométricas básicas.
• Ejemplos de ecuaciones trigonométricas:
  • sin x + sin 2x = 1/2; tan x + cot x = 1,732;
  • cos 3x + sen 2x = cos x; 2sin 2x + cos x = 1.

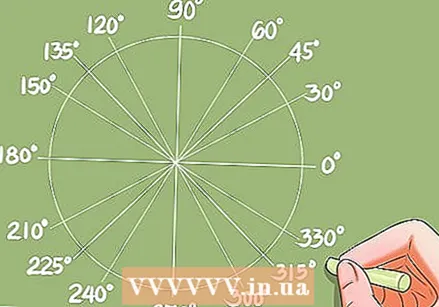
1. El círculo unitario.
   • Este es un círculo con Radio = 1, donde O es el origen. El círculo unitario define 4 funciones trigonométricas principales de la curva variable x, que la rodea en sentido antihorario.
   • Cuando la curva con valor x varía en el círculo unitario, entonces se mantiene:
   • El eje horizontal OAx define la función trigonométrica f (x) = cos x.
   • El eje vertical OBy define la función trigonométrica f (x) = sen x.
   • El eje vertical AT define la función trigonométrica f (x) = tan x.
   • El eje horizontal BU define la función trigonométrica f (x) = cot x.

• El círculo unitario también se usa para resolver ecuaciones trigonométricas básicas y desigualdades trigonométricas estándar considerando las diversas posiciones de la curva x en el círculo.

Al paso

1. Comprende el método de solución.
   • Para resolver una ecuación trigonométrica, conviértala en una o más ecuaciones trigonométricas básicas. Resolver ecuaciones trigonométricas finalmente da como resultado la solución de 4 ecuaciones trigonométricas básicas.
2. Saber resolver ecuaciones trigonométricas básicas.
   • Hay 4 ecuaciones trigonométricas básicas:
   • sen x = a; cos x = a
   • tan x = a; cuna x = a
   • Puede resolver las ecuaciones trigonométricas básicas estudiando las distintas posiciones de la curva x en el círculo trigonométrico y utilizando una tabla de conversión trigonométrica (o calculadora). Para comprender completamente cómo resolver estas y otras ecuaciones trigonométricas básicas similares, lea el siguiente libro: "Trigonometría: resolución de ecuaciones trigonométricas y desigualdades" (Amazon E-book 2010).
   • Ejemplo 1. Resuelva para sen x = 0.866. La tabla de conversión (o calculadora) da la respuesta: x = Pi / 3. El círculo trigonométrico da otra curva (2Pi / 3) con el mismo valor para el seno (0.866). El círculo trigonométrico también proporciona una infinidad de respuestas llamadas respuestas extendidas.
   • x1 = Pi / 3 + 2k.Pi y x2 = 2Pi / 3. (Respuestas dentro de un período (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi y x2 = 2Pi / 3 + 2k Pi. (Respuestas detalladas).
   • Ejemplo 2. Resuelva: cos x = -1/2. Las calculadoras dan x = 2 Pi / 3. El círculo trigonométrico también da x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi y x2 = - 2Pi / 3. (Respuestas para el período (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi y x2 = -2Pi / 3 + 2k.Pi. (Respuestas extendidas)
   • Ejemplo 3. Resuelva: tan (x - Pi / 4) = 0.
   • x = Pi / 4; (Respuesta)
   • x = Pi / 4 + k Pi; (Respuesta extendida)
   • Ejemplo 4. Resuelva: cot 2x = 1.732. Las calculadoras y el círculo trigonométrico dan:
   • x = Pi / 12; (Respuesta)
   • x = Pi / 12 + k Pi; (Respuestas extendidas)
3. Aprenda las transformaciones que se utilizan para resolver ecuaciones trigonométricas.
   • Para convertir una ecuación trigonométrica dada en ecuaciones trigonométricas estándar, use conversiones algebraicas estándar (factorización, factor común, polinomios ...), definiciones y propiedades de funciones trigonométricas e identidades trigonométricas. Hay alrededor de 31, 14 de las cuales son identidades trigonométricas, de 19 a 31, también llamadas identidades de transformación, porque se utilizan en la conversión de ecuaciones trigonométricas. Vea el libro de arriba.
   • Ejemplo 5: La ecuación trigonométrica: sin x + sin 2x + sin 3x = 0 se puede convertir en un producto de ecuaciones trigonométricas básicas usando identidades trigonométricas: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Las ecuaciones trigonométricas básicas a resolver son: cos x = 0; sin (3x / 2) = 0; y cos (x / 2) = 0.
4. Encuentre las curvas para las que se conocen las funciones trigonométricas.
   • Antes de que pueda aprender a resolver ecuaciones trigonométricas, necesita saber cómo encontrar rápidamente las curvas para las que se conocen las funciones trigonométricas. Los valores de conversión de curvas (o ángulos) se pueden determinar con tablas trigonométricas o con la calculadora.
   • Ejemplo: Resuelva para cos x = 0.732. La calculadora da la solución x = 42,95 grados. El círculo unitario da otras curvas con el mismo valor para el coseno.
5. Dibuja el arco de la respuesta en el círculo unitario.
   • Puede crear una gráfica para ilustrar la solución en el círculo unitario. Los puntos finales de estas curvas son polígonos regulares en el círculo trigonométrico. Algunos ejemplos:
   • Los puntos finales de la curva x = Pi / 3 + k. Pi / 2 es un cuadrado en el círculo unitario.
   • Las curvas de x = Pi / 4 + k.Pi / 3 están representadas por las coordenadas de un hexágono en el círculo unitario.
6. Aprenda a resolver ecuaciones trigonométricas.
   • Si la ecuación trigonométrica dada contiene solo una función trigonométrica, resuélvala como una ecuación trigonométrica estándar. Si la ecuación dada contiene dos o más funciones trigonométricas, hay 2 métodos de solución, dependiendo de las opciones para convertir la ecuación.
     • A. Método 1.
   • Convierta la ecuación trigonométrica a un producto de la forma: f (x) .g (x) = 0 o f (x) .g (x) .h (x) = 0, donde f (x), g (x) y h (x) son ecuaciones trigonométricas básicas.
   • Ejemplo 6. Resuelva: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Solución. Reemplaza sin 2x en la ecuación usando la identidad: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Luego, resuelva 2 funciones trigonométricas estándar: cos x = 0 y (sin x + 1) = 0.
   • Ejemplo 7. Resuelva: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • Solución: Convierta esto en un producto, usando las identidades trigonométricas: cos 2x (2cos x + 1) = 0. Ahora resuelva las 2 ecuaciones trigonométricas básicas: cos 2x = 0 y (2cos x + 1) = 0.
   • Ejemplo 8. Resuelva: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Solución: Convierta esto en un producto, usando las identidades trigonométricas: -cos 2x * (2sin x + 1) = 0. Ahora resuelva las 2 ecuaciones trigonométricas básicas: cos 2x = 0 y (2sin x + 1) = 0.
     • B. Enfoque 2.
   • Convierte la ecuación trigonométrica en una ecuación trigonométrica con una única función trigonométrica como variable. Hay algunos consejos sobre cómo elegir una variable adecuada. Las variables comunes son: sen x = t; cos x = t; cos 2x = t, tan x = t y tan (x / 2) = t.
   • Ejemplo 9. Resuelva: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Solución. En la ecuación, reemplace (cos ^ 2x) con (1 - sin ^ 2x) y simplifique la ecuación:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Ahora usa sin x = t. La ecuación se convierte en: 5t ^ 2 - 4t - 9 = 0. Esta es una ecuación cuadrática con 2 raíces: t1 = -1 y t2 = 9/5. Podemos rechazar el segundo t2, porque> 1. Ahora resuelva para: t = sin = -1 -> x = 3Pi / 2.
   • Ejemplo 10. Resuelva: tan x + 2 tan ^ 2 x = cot x + 2.
   • Solución. Utilice tan x = t. Convierta la ecuación dada en una ecuación con t como variable: (2t + 1) (t ^ 2 - 1) = 0. Resuelva para t a partir de este producto, luego resuelva la ecuación trigonométrica estándar tan x = t para x.
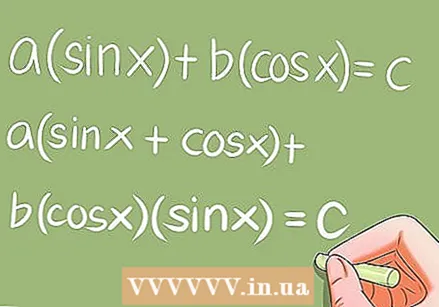7. Resolver ecuaciones trigonométricas especiales.
   • Hay algunas ecuaciones trigonométricas especiales que requieren algunas conversiones específicas. Ejemplos:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
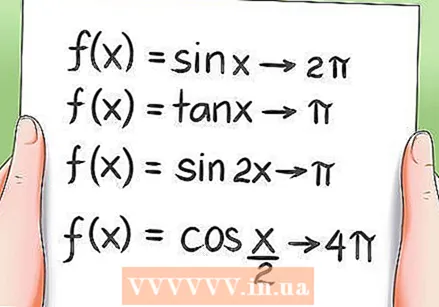8. Aprenda las propiedades periódicas de las funciones trigonométricas.
   • Todas las funciones trigonométricas son periódicas, lo que significa que vuelven al mismo valor después de una rotación durante un período. Ejemplos:
     • La función f (x) = sen x tiene 2Pi como período.
     • La función f (x) = tan x tiene Pi como período.
     • La función f (x) = sen 2x tiene Pi como período.
     • La función f (x) = cos (x / 2) tiene 4Pi como período.
   • Si el período se especifica en los ejercicios / prueba, entonces solo necesita encontrar la (s) curva (s) x dentro de este período.
   • NOTA: Resolver ecuaciones trigonométricas es complicado y, a menudo, conduce a errores y equivocaciones. Por lo tanto, las respuestas deben revisarse cuidadosamente. Después de resolver, puede verificar las respuestas usando una calculadora gráfica, para obtener una representación directa de la ecuación trigonométrica dada R (x) = 0. Las respuestas (como raíz cuadrada) se dan en lugares decimales. Como ejemplo, Pi tiene un valor de 3,14